Whereas the norm of the matrix provides a way to measure the magnitude of the matrix, the condition number of a matrix is a measure of how close the matrix is to being singular. The condition number of a square nonsingular matrix is defined as
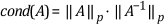
where p can be one of the four norm types previously described. For example, to find the condition number of a matrix A, you can find the 2-norm of A, the 2-norm of the inverse of the matrix A, denoted by A-1, and then multiply them together. The inverse of a square matrix A is a square matrix B such that AB = I, where I is the identity matrix.
For example,
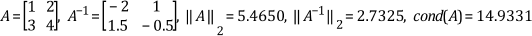
The condition number can vary between 1 and infinity. A matrix with a large condition number is nearly singular, while a matrix with a condition number close to 1 is far from being singular. The matrix A is nonsingular. However, consider the matrix
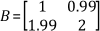
The condition number of this matrix is 47,168, and hence the matrix is close to being singular. A matrix is singular if its determinant is equal to zero. However, the determinant is not a good indicator for assessing how close a matrix is to being singular. For the matrix B, the determinant (0.0299) is nonzero. However, the large condition number indicates that the matrix is close to being singular. Remember that the condition number of a matrix is always greater than or equal to one; the latter being true for identity and permutation matrices. A permutation matrix is an identity matrix with some rows and columns exchanged. The condition number is a very useful quantity in assessing the accuracy of solutions to linear systems.