Funktionen untersuchen
Integral- und Differentialrechnung
Oft musst du für eine Funktion Dinge wie Nullstellen, Minima oder Integrale bestimmen. Auch dafür stehen Befehle zur Verfügung. Allerdings musst du dafür die Funktion die du untersuchen möchtest erst in einem m-File definieren.
% testFun.m function y = testFun(x) y = sin(x).*cos(x).^2; endfunction
Ist die Funktion definiert, kannst du die folgenden Befehle verwenden um sie zu untersuchen.
ezplot('testFun(x)') | Die Funktion testFun darstellen |
fminbnd('testFun', min,max) | Bestimmt das Minimum von testFun zwischen min und max |
fzero('testFun', start) | Bestimmt eine Nullstelle von testFun in der Nähe von start |
quad('testFun', min,max) | Integriert testFun zwischen min und max |
quadl('testFun', min,max) | Integriert testFun zwischen min und max |
Aufgabe 1
Untersuche die Funktion testFun mit den Befehlen oben.
- Bestimme alle Minima zwischen 0 und 3.
- Bestimme alle Nullstellen zwischen -2 und 2.
- Bestimme das Integral zwischen 1 und 3.
- Zeichne die Funktion.
Definiere anschliessend selbst einen Funktion und untersuche diese ebenfalls. Wie könntest du die Maxima einer Funktion bestimmen?
x = -5:0.1:5; plot(x, testFun(x)); disp('Minima') fminbnd('testFun', 0, 3); disp('Nullstellen') fzero('testFun', 0); disp('Integral') quad('testFun', 1, 3);
Gewöhnliche Differential Gleichungen
In der Physikvorlesung solltest du gelernt haben, wie du eine Differentialgleichung analytisch lösen kannst. Dies ist nicht immer möglich. Numerisch lässt sich aber immer eine Näherungslösung finden.
Als Beispiel betrachten wir hier den Schiefen Wurf ohne Luftwiderstand.
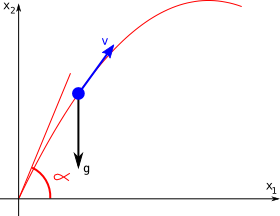
Gegeben seien die Anfangsbedingungen:

Um dieses Problem numerisch zu lösen, teilen wir den Weg in viele kleine Schritte und berechnen
jeweils den Ort und die Geschwindigkeit nach einem Abschnitt.
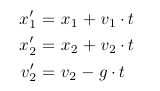
Aufgabe 2
Implementiere die oben beschriebene Methode um den Schiefen Wurf zu berechnen. Speichere dazu Ort, Geschwindigkeit und Beschleunigung in drei Vektoren x, v, a und aktualisiere diese nach jedem Schritt mit den neuen Werten. Zeichne in jedem Schritt einen Punkt für den aktuellen Ort. Variiere am Ende die Schrittlänge und schaue welchen Effekt das hat.
Für dieses Problem kennst du auch die analytische Lösung:
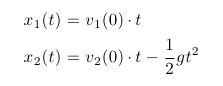
Zeichne diese ebenfalls ein und vergleiche mit den verschieden Versionen deiner numerischen Lösung.
Den Code für diese Aufgabe solltest du selbst schreiben können.
Das Resultat sollte ungefähr wie unten aussehen.
Wie üblich gilt: Melde dich, wenn du nicht weiter kommst.
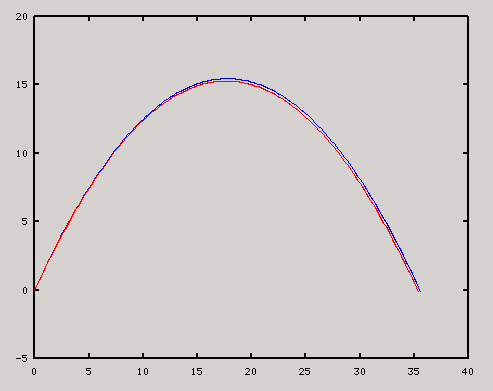
Wie du siehst, bekommen wir mit unserer Methode keine schlechten Resultate. Wir liegen aber systematisch über dem korrekten Resultat. Es gibt deshalb weitere, bessere Algorithmen um Differential-Gleichungen zu lösen. Du musst diese Algorithmen aber nicht selbst programmieren.
lsode (octave) / ode45 (matlab)
lsode und ode45 sind Befehle, mit denen du Differentialgleichungen
lösen kannst.
Wir wollen den Schiefen Wurf nun auch mit diesen lösen.
Als erstes müssen wir unser Problem durch eine Funktion beschreiben.
Die Funktion muss zwei Argumente haben.
Einen Vektor mit den den momentanen Werten deiner Grössen (x,v,a)
sowie ein Zeitintervall.
Der Rückgabewert deiner Funktion ist dann die Veränderung der Werte während diesem Schritt.
Aufgabe 3
Passe die Funktion unten so an, dass sie den Schiefen Wurf beschriebt. Ändere deinen Code aus Aufgabe 2 anschliessend so ab, dass er diese Funktion verwendet und kontrolliere, dass noch alles Funktioniert.
% X(1) = x, X(2) = y % X(3) = vx, X(4) = vy % X(5) = ax, X(6) = ay function xDot = schieferWurf(X,t) % Octave function xDot = schieferWurf(t,X) % Matlab xDot(1) = ... xDot(2) = ... xDot(3) = ... xDot(4) = ... xDot(5) = ... xDot(6) = ... xDot = xDot' % nur Matlab
% schieferWurf.m function xDot = schieferWurf(X,t) % Octave function xDot = schieferWurf(t,X) % Matlab xDot(1) = t*X(3); xDot(2) = t*X(4); xDot(3) = 0; xDot(4) = -t*X(6); xDot(5) = 0; xDot(6) = 0; xDot = xDot' % nur Matlab
Wenn du diese Funktion hast, kannst du lsode bzw. ode45 verwenden
um das Problem zu lösen
% octave xOut = lsode('schieferWurf', [0 0 v_1 v_2 0 g], [0:0.1:3]) % matlab [tOut, xOut] = ode45('schieferWurf',... [0:0.1:3], [0 0 v_1 v_2 0 g])
Die Argumente sind jeweils
'schieferWurf'der Name deiner Funktion[0 0 v_1 v_2 0 g]die Anfangswerte[0:0.1:3]die gewünschten Zeiten für die Auswertung.
In Matlab kannst du auch nur Start- und Endzeit angeben ([0 3])
xOut ist in beiden Programmen eine Matrix deren Zeilen die X-Werte für die Auswertungspunkte enthalten. Bei Matlab bekommst du diese in tOut ebenfalls zurück.
Aufgabe 4
Verwende deine Funktion und lsode bzw. ode45 um die Lösung für unser Problem zu bestimmen.
Stelle anschliessend diese gemeinsam mit der analytischen Lösung dar.
Hinweis: Mit A(:,1) wählst du die 1. Spalte, mit A(3,:) die 3. Zeile der Matrix A aus.
v = 20; g = 9.81; alpha = 60; dt = 0.02; vx =v*cos(alpha/180*pi); vy =v*sin(alpha/180*pi); % numerisch xOut = lsode('schieferWurf', [0 0 vx vy 0 g], [0:0.1:3]); plot(xOut(:,1), xOut(:,2)) hold on % analytisch j = 1; yAnalytic=0; xAnalytic=0; while yAnalytic(j) >= 0 t = dt*j; xAnalytic(j+1) = vx*t; yAnalytic(j+1) = vy*t-0.5*g*t^2; j = j+1; end plot(xAnalytic, yAnalytic, 'r') hold off
