Das Grundwissen
Hilfe erhalten
Tipp: Auf den nächsten Seiten wirst du viele Octave/Malab Befehle lernen. Niemand erwartet, dass du dir diese alle merken kannst. Deshalb sind Referenzen wie sie unten auf der Übersichtsseite verlinkt sind sehr nützlich. Am besten Druckst du dir das Cheetsheet jetzt gleich aus.
help
Mit dem Befehl help kannst du dir eine kurze Hilfe zu verschiedensten
Themen anzeigen lassen. Versuche die folgenden Befehle
help help help help + help sqrt
Du siehst help funktioniert ähnlich, wie man in der Shell.
lookfor
lookfor ist das Analogon zu apropos in der Shell.
Du kannst damit also nach einem Befehl oder Operator zu einem bestimmten Begriff suchen.
Tippe zum Beispiel
lookfor plot
um alle Themen die mit plot zu tun haben anzuzeigen.
info
Schliesslich gibt es auch noch den Befehl info. Dieser hat in Matlab und
Octave unterschiedliche Effekte. In Matlab funktioniert er wie help, gibt
aber eine ausführlichere Beschreibung aus. In Octave erhältst du mit info
Verweise auf Websites mit weiteren Informationen.
Verzeichnisse
Auch innerhalb von Matlab und Octave kannst du durch deinen Verzeichnisbaum navigieren. Wichtig ist insbesondere das aktive Verzeichnis. Denn wenn du eine Datei speicherst, wird sie im aktiven Verzeichnis erstellt. Auch wenn du ein m-File ausführen möchtest, wird zuerst im aktiven Verzeichnis nach der entsprechenden Datei gesucht. (Zu beidem später mehr.)
Navigationsbefehle
Beide Programme verstehen die bereits aus der Shell bekannten Befehle. Probiere die Befehle
ls, cd, pwd.
Nützliche Befehle
diary
Mit dem Befehl diary oder diary on kannst du aufzeichnen lassen,
was passiert. Alle Eingaben und Ausgaben werden in die Datei diary im aktiven Verzeichnis
gespeichert. Die weitere Optionen zu diary und wie du die Aufzeichnung wieder ausschaltest, erklärt
die Hilfe. Starte für die nächsten Befehle nun aber erst einmal die Aufzeichnung:
diary on
whos
Damit du den Effekt der nächsten Befehle sehen kannst, musst du nun erst ein paar Variablen definieren.
a = 10 b = 6
Mit whos kannst du dir nun eine Liste aller existierenden Variablen
ausgeben lassen. Natürlich kann auch whos noch mehr, doch du weisst
nun ja, wo du die Erklärungen findest.
clear
clear erlaubt es dir eine oder mehrere Variablen zu löschen.
whos clear a whos antwort = 42 whos clear
clc
Um herauszufinden, was clc macht, tippst du es am besten ein
und/oder schaust dir die Hilfe an.
Du kannst nun diary wieder ausschalten. Schau dir anschliessend die
resultierende Datei in der Shell an. (z.B. mit less
Vektoren & Matrizen
Als nächstes werden wir nun elementare Matrizen-Operationen einführen. Eine Matrix definierst du zum Beispiel so
A = [ 1 2 3; 4 5 6 ]
Wie du siehst, erzeugt das eine 2x3 Matrix. Du gibst die Matrizen also zeilenweise ein. Zeilen beendest du mit einem Strichpunkt (;).
Aufgabe 1
Gib die folgenden Vektoren und Matrizen ein
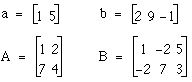
a=[1 5] b=[2 9 -1] A=[1 2;7 4] B=[1 -2 5;-2 7 3]
Variablen speichern und laden
Wenn du regelmässig die gleichen Variablen benötigst, so möchtest du diese natürlich nicht jedes Mal eintippen. Deshalb kannst du einzelne oder alle Variablen deines Workspace speichern.
whos save myVars A B clear A B whos
Du hast nun die Matrizen A und B in die Datei myVars gespeichert. Schau dir diese Datei in der Shell an.
Da wir die beiden Matrizen nach dem Speichern gelöscht haben, müssen wir sie nun auch wieder neu laden.
load myVars whos
Aufgabe 2
Definiere zusätzlich zu den bestehenden Variablen noch
c = [ -2 3 5 ]
Verwende dann die Operatoren * (mal), ^ (hoch) und ' (transponieren) sowie die Funktionen cross und dot um folgende Matrix-Operationen auszuführen:
- aB
- BTaT
- bBT
- BBT
- BTB
- A2
- Skalarprodukt von c und b (hier gibt es zwei Lösungen)
- Vektorprodukt von b und c
a*B B'*a' b*B' B*B' B'*B A^2 dot(c,b) % Lösung 1 c*b' % Lösung 2 cross(b,c)
Aufgabe 3
Aus der Linearen Algebra solltest du wissen, wie man mit Matrizen ein Gleichungssystem
lösen kann. Stelle das Gleichungssystem
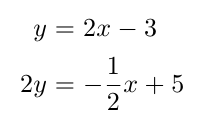
als Matrizen-Gleichung der Form Ax = b dar und bestimme x.
Tipp: Die zu A inverse Matrix bekommst du mit inv(A)
A = [ -2 1 ; .5 2 ] b = [ -3; 5] inv(A) * b % oder A \ b
Aufgabe 4
Um besondere Matrizen einfach eingeben zu können bestehen extra Funktionen. Verwende die
Funktionen eye, zeros und ones um folgenden
Matrizen einzugeben:
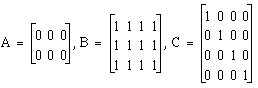
A = zeros(2,3) B = ones(3,4) C = eye(4)
Komplexe Zahlen
Falls du bisher nichts von Komplexen Zahlen gehört hast, so schaue dir die Erklärung auf MathWorld an und/oder melde dich bei uns.
Die imaginäre Einheit ist i. Du kannst eine komplexe Zahl also wie erwartet definieren.
z = 3 + 2i
Achtung: i ist kein geschützter Name. Du kannst eine eigene Variable i definieren, die dann die imaginäre Einheit ersetzen kann! Du solltest deshalb die imaginäre Einheit immer mit einer vorangestellten Zahl verwenden.
Aufgabe 5
Definiere die folgenden komplexen Variablen zi = xi+yii im Command Window
- z1 = 3+4i
- z2 = 1-7i
- z3 =
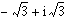
Verwende die Funktionen conj, real, imag, abs, angle sowie atan und berechne von z1, z2 und z3 jeweils die konjugiert komplexe Zahl und die Polarform.
Normalform: z = x + iy
Polarform: z = ![]() (cos
(cos![]() +
isin
+
isin![]() )
)
Radius ![]() :
:
![]()
Winkel ![]() :
:
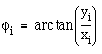
z1=3+4i z2=1-7i z3=-sqrt(3)+1i*sqrt(3) conj(z1) % entweder z1' % oder conj(z2) % entweder z2' % oder conj(z3) % entweder z3' % oder rho1=sqrt(real(z1)^2+imag(z1)^2) % entweder rho1=abs(z1) % oder phi1=atan(imag(z1)/real(z1)) % entweder phi1=angle(z1) % oder rho2=sqrt(real(z2)^2+imag(z2)^2) % entweder rho2=abs(z2) % oder phi2=atan(imag(z2)/real(z2)) % entweder phi2=angle(z2) % oder rho3=abs(z3) phi3=angle(z3)
Aufgabe 6
Führe folgende Operationen aus und kontrolliere, dass du jeweils für die Normal- und die Polarform auf die gleichen Resultate kommst.
- Addition zweier komplexen Zahlen:
- z1 + z2 = ?
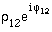 = ?
= ?
- Multiplikation zweier komplexer Zahlen:
- z1z2 = ?
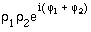 = ?
= ?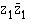 = ?
= ?- |z1| = ?
- Division zweier komplexer Zahlen:
- z1/z2 = ?
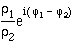 = ?
= ?- 1/z1 = ?
- z1normiert =
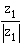 = ?
= ? - 1/z1normiert = ?
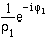 = ?
= ?
- Potenzieren einer komplexen Zahl (Moivresche Formel):
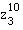 = ?
= ?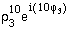 = ?
= ?
- Radizieren einer komplexen Zahl:
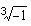 = ?
= ?
%Addition z1+z2 rho12=sqrt(rho1^2+rho2^2+2... *rho1*rho2*cos(phi1-phi2)) phi12=atan((rho1*sin(phi1)+rho2*sin(phi2))/... (rho1*cos(phi1)+rho2*cos(phi2))) rho12*exp(i*phi12) % Multiplikation z1*z2 rho1*rho2*exp(1i*(phi1+phi2)) z1*conj(z1) % entweder z1*z1' % oder abs(z1) % entweder sqrt(z1*z1') % oder % Division z1/z2 (rho1/rho2)*exp(1i*(phi1-phi2)) 1/z1 z1normiert=z1/abs(z1) 1/z1normiert 1/rho1*exp(-1i*phi1) % Potenzieren einer komplexen Zahl z3^10 rho3^10*exp(1i*(10*phi3)) % Radizieren -1^(1/3) (-1)^(1/3) rho=abs(-1) phi=angle(-1) ls1=rho^(1/3)*exp(1i*(phi/3)) ls2=rho^(1/3)*exp(1i*((phi+2*pi)/3)) ls3=rho^(1/3)*exp(1i*((phi+4*pi)/3))
Aufgabe 7
Welche Funktion dreht die komplexe Zahlenebene um den Winkel 90 Grad? Verifiziere dies mit der komplexen Zahl z1.
phiz1=angle(z1)*180/pi w1=1i*z1 phiw1=angle(w1)*180/pi
