Entropy is a measure of how disordered a system is. The total entropy in the universe always increases (or, at best, remains constant). Consider a sealed room with a hot cup of tea in it. The tea will tend to lose heat to the surrounding air, making the air molecules move faster. This makes the whole system more disordered, as faster moving molecules are less ordered than slower ones. No energy is lost from the system, but there is an increase in entropy. The more disordered a system is, the more information is needed to describe it. Consider again the room with the cup of tea. When the molecules are heated by the tea, they move faster. It takes more information to describe the exact state of all the faster-moving molecules than it did when they were moving more slowly. This is because each individual molecule, as it can now move faster, has a bigger range of speeds it can be travelling at while the air and tea are in thermodynamic equilibrium. As there are more possible microstates (positions and speeds of individual molecules), it takes more information to describe the system.
It is possible to calculate entropy using the equation:
S = k ln W
where S is entropy, k is Boltzmann's constant (1.38 x 10-23 J/K), and W is the number of possible microstates which correspond to the desired macrostate (e.g. the tea being the same temperature as the air in the room). (This equation is in The Physical Universe by Prof. Frank H. Shu).
In my calculations, however, I used that equation along with another equation:
S/t = Power/Temperature
and the fact that:
Information (in bits) = log2 W
I used these equations to calculate the entropy and information gained in various processes: A cup of tea cooling, a human respiring, an earthquake, the Earth re-radiating energy from the Sun, the Sun "burning" hydrogen and a quasar radiating energy.
Using a human as an example, I will show how I calculated the entropy and information gained in these processes.
A human uses approx. 2000 kcal per day. 1 cal is 4.2 J. Therefore the power of a human is 2 x 106 x 4.2 J/day = 8.4 x 106 J/day. As there are 86 400 seconds in a day, power = (8.4 x 106)/86 400 W which is approx. 100 W.
Room temperature is about 300 K, so S/t = Power/temperature = 100/300 = 0.33 JK-1sec-1.
(ln W)/t = (1/k) x (S/t) = 0.33/(1.38 x 10-23) = 2.4 x 1022
To turn my answer for (ln W)/t into bits/sec, I must divide by ln 2:
(2.4 x 1022)/ln 2 = 3.5 x 1022 bits/sec
For the cup of tea, I used a different method:
integrate (1/T, T = 300 K . . . 373 K) x specific heat capacity of water x mass of tea
This gives: ln (373/300) x 4.2 x 300 = 274 JK-1 and so ln W = 274/(1.38 x 10-23) = 2.0 x 1025 which in bits is (2.0 x 1025)/ln 2 = 2.9 x 1025 bits
Some of the processes I used are continuous (human, Sun, quasar and Earth) and the others are discrete (earthquake and cup of tea). For the discrete processes, I used S = energy/temperature. Also, for the Earth re-radiating energy from the Sun, I made some assumptions. I assumed that, as the Sun shone unequally on the Earth (the Sun shines more strongly at noon), I would model the Earth as a disc (so the surface area was less) and I would use the fact that at noon, the Earth absorbs 1 kWm-2. I calculated the information received frrom the Sun, and then the information given out by the Earth (which would be greater as the temperature at night is less (I assumed it was 15 K less)). I then calculated the difference, and it was this value I used.
So that you can calculate the rest for yourselves, checking them against my answers in the table below, I shall provide you with the numbers I used, and where I got them from.
Radius of the Earth = 6.37 x 106 m (from The Physical Universe )
Temperature of Earth during the day = 300 K and at night = 285 K
Effective temperature of the Sun = 5 800 K ( The Physical Universe )
Luminosity (power) of the Sun = 3.9 x 1026 W ( The Physical Universe )
Effective temperature of a quasar = 106 K ( The Physical Universe )
Luminosity of a quasar = 1040 W ( The Physical Universe )
Energy of an earthquake (in ergs) = 10(11.8 + 1.5M) where M is the magnitude on the Richter scale (I used M = 7).( 1 J = 107 erg). (from What is Richter Magnitude? )
| Object | Entropy | Information |
| Human | 0.33 | 3.5 x 1022 |
| Cup of tea | 274 | 2.9 x 1025 |
| Earthquake | 6.7 x 1013 | 7.1 x 1036 |
| Earth | 7.0 x 1013 | 7.4 x 1036 |
| Sun | 6.7 x 1022 | 4.9 x 1045 |
| Quasar | 1.0 x 1034 | 1.0 x 1057 |
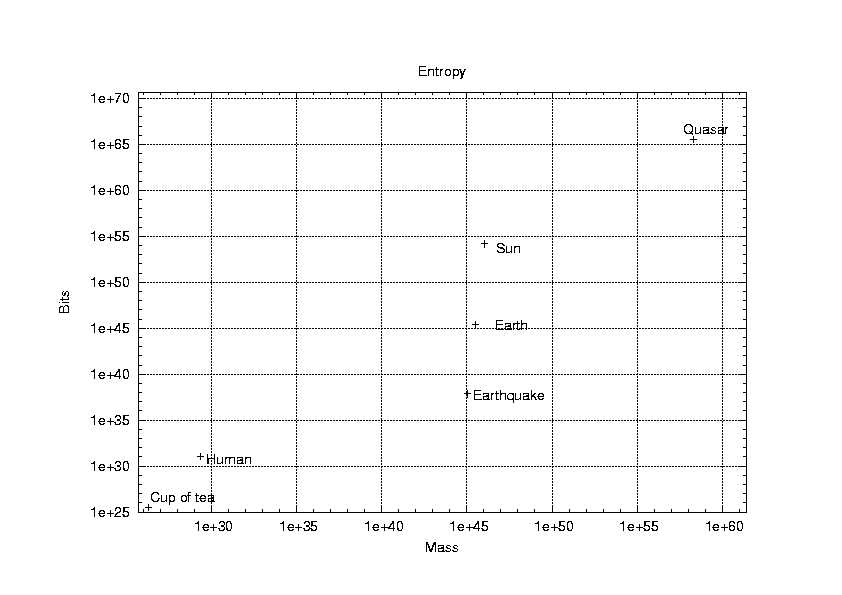
I then decided to compare the results on a graph with the information (in bits) against mass. I decided also to look at the continuous processes over the course of one year (rather than one second), which meant I multiplied my answers by 3.1536 x 108. In some cases I had to calculate the mass, and in others, I found it directly.
For a human, I estimated that approx. 1 kg is consumed each day. That means 365 kg is consumed in one year. I calculated how many protons would be needed to make up that mass (that is the unit of my mass calculation). 1 proton has a mass of 1.67 x 10-24 g (from The Physical Universe ). So the mass a human consumes in a year is 365 000/(1.67 x 10-24) = 2.2 x 1029
For the cup of tea, the mass was 300 g, and for the Earth I used the mass of the atmosphere (as I assumed that was what was absorbing and re-radiating most of the heat) which is 5.1 x 1021 g (from Earth's atmosphere ). For the Sun I used the mass of hydrogen burnt, which I calculated using the luminosity of the Sun and the binding energy per helium nucleus. The binding energy per helium nucleus is 4.54 x 10-12 J (from Nuclear binding energy ) and m = (3.9 x 1026)/(4.54 x 10-12) = 8.6 x 1037 He/sec. If you multiply this by four, you get the mass as 3.4 x 1038 protons/sec which is 1.1 x 1046 protons/year.
For the earthquake I assumed that the part of the Earth taking part in the earthquake was a section of the crust with radius 100 km. As the crust is 20 km thick, the volume of the crust is 3.14 x 1002 x 20 = 6.28 x 105 km3 which is 6.28 x 1020 cm3. The density of the crust is 2.8 g cm-3 (from The Geologic Earth ) therefore the mass is 6.28 x 1020 x 2.8 = 1.8 x 1021 g.
The Physical Universe says that, for a quasar, about 10 % of the mass is converted into energy. Therefore, as we know the energy output in one year, we can calculate the mass using E = m c2, or to find out the mass, m = E/c2, and then muptiply this by 10 to get the mass in kg and then by 1000 to get the mass in g. m = 1.2 x 1046 and so the total mass is 1.2 x 1046 x 10 x 1000 = 1.2 x 1050 g
| Object | Mass | Information |
| Cup of tea | 2.0 x 1026 | 2.9 x 1025 |
| Human | 2.2 x 1029 | 1.1 x 1031 |
| Earthquake | 1.1 x 1045 | 7.1 x 1037 |
| Earth | 3.1 x 1045 | 2.3 x 1045 |
| Sun | 1.1 x 1046 | 1.5 x 1054 |
| Quasar | 2.1 x 1058 | 3.2 x 1065 |

As you can see from the graph, they all lie on pretty much the same straight line, except for the Earth and earthquake. This is probably because the mass I used for both is more than the mass which was actually involved.