IPython und ein Physik-Beispiel
Tipp: Du hast bereits diverse Python-Befehle kennen gelernt und wirst noch viele weitere Befehle lernen. Niemand erwartet, dass du dir diese alle merken kannst. Deshalb sind Referenzen wie sie unten auf der Übersichtsseite verlinkt sind sehr nützlich. Am besten Druckst du dir das Cheatsheet jetzt gleich aus.
ipython und pylab
Im letzten Block hast du die Python-Shell kennengelernt. Sie reicht für alle Aufgaben dieses Tutorials. Mit IPython steht jedoch auch eine verbesserte Python-Shell zur Verfügung. IPython ist optimiert für interaktives Arbeiten und bietet viele nützliche Optionen. Für den Moment ist insbesondere pylab interessant. Pylab lädt verschiedene Module die fürs Auswerten von Daten nützlich sind und stellt sicher, dass diese sauber zusammenspielen. Wir verwenden deshalb für dien Kurs von jetzt an stets Pylab.
Beende deshalb nun eine allfällige Python-Shell ([ctrl]+[d]).
Danach tippst du folgenden Befehl um IPython mit pylab zu starten:
ipython3 --pylab=qt4
Hinweis: Im Befehl oben legen wir auch das Grafik-Backend von pylab fest (qt4). Um den Befehl zu vereinfachen, kannst du das Backend auch in der Konfigurationsdatei von Matplotlib festlegen.
Dafür führst du in der Shell folgende Zeile aus
echo "backend : QT4Agg" >> ~/.config/matplotlib/matplotlibrc
Danach kannst du pylab mit ipython3 --pylab starten.
Nach den einführenden Bemerkungen erhältst du nun einen neuen Prompt. Auch hier funktioniert alles, was du im letzten Abschnitt gelernt hast. Wie versprochen sind diverse Module bereits geladen. So hast du zum Beispiel direkt zugriff auf die math-Funktionen
sqrt(2) e
Ausserdem kannst du in IPython mit Out[n] auf das
Resultat deines n-ten Befehl zugreifen.
Versuche nun einige Rechnungen zum Beispiel die aus dem letzten Block oben.
Hilfe erhalten
Auch die normale Python-Hilfe ist in IPython verfügbar.
help(sqrt)
Die Ausgabe ist aber sehr allgemein und nicht spezifisch für die Wurzelfunktion.
Wie im Hilfetext erwähnt, kannst du die Hilfe zu einzelnen Funktionen aber mit
np.info(sqrt) anzeigen lassen.
Die einführenden Bemerkungen von IPython haben dich zudem auf
object? hingewiesen.
Mit ? bekommst du auch hier eine nützlichere
Erklärung.
sqrt?
Mit Variablen arbeiten
Damit du den Effekt der nächsten Befehle sehen kannst, musst du nun erst ein paar Variablen definieren.
a = 3 b = 4 c = 5 %whos
In IPython kannst du dir mit %whos eine Liste aller existierenden Variablen
ausgeben lassen.
%whos ist ein Magic-Function von IPython.
Magic-Functions sind IPython spezifisch.
Sie beginnen mit einem % und bieten viele nützliche Funktionen.
Eine Liste der verfügbaren Magic-Functions findest du in der quickref.
Wir werden die wichtigsten aber auch im Verlaufe dieses Kurses kennenlernen.
Um eine oder mehrere bestehende Variablen zu löschen, kannst du del verwenden.
del a,b %whos
Shell-Befehle
Wie in der Shell, hast du auch in Python ein aktives Arbeitsverzeichnis.
Beim Start wird das aktive Arbeitsverzeichnis deiner Shell übernommen.
Um im Verzeichnisbaum zu navigieren, kannst du in IPython die Befehle
verwenden, die du aus der Shell kennst:
pwd, cd, ls
Auch sonst stehen diverse Shell-Befehle zur Verfügung.
Falls nicht, so kannst IPython beauftragen einen Befehl in der Shell auszuführen,
indem du die Zeile mit einem ! beginnst.
Komplexe Zahlen
Du kennst nun die Grundlagen für die Bedienung von Python. Wir wollen dieses Wissen nun anwenden um ein paar Aufgaben mit komplexen Zahlen zu lösen.
Falls du bisher nichts von Komplexen Zahlen gehört hast, so schaue dir die Erklärung auf MathWorld an und/oder melde dich bei uns.
Die imaginäre Einheit ist in python 1j.
Damit kannst eine komplexe Zahl wie erwartet definieren.
z = 3 + 2j
Die Hilfe zu komplexen Zahlen kannst du dir mit help('COMPLEX') anzeigen lassen.
Aufgabe 1
Definiere die folgenden komplexen Variablen zi = xi+yii im Command Window
- z1 = 3+4i
- z2 = 1-7i
- z3 =
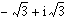
Verwende die Funktionen conj, real, imag, abs, angle sowie arctan und berechne von z1, z2 oder z3 die konjugiert komplexe Zahl und die Polarform.
Normalform: z = x + iy
Polarform: z = ![]() (cos
(cos![]() +
i*sin
+
i*sin![]() )
)
Radius ![]() :
:
![]()
Winkel ![]() :
:
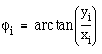
z1=3+4j z2=1-7j z3=-sqrt(3)+1j*sqrt(3) conj(z1) # entweder z1.conjugate() # oder conj(z2) # entweder z2.conjugate() # oder conj(z3) # entweder z3.conjugate() # oder rho1=sqrt(real(z1)**2+imag(z1)**2) # entweder rho1=abs(z1) # oder phi1=arctan(imag(z1)/real(z1)) # entweder phi1=angle(z1) # oder rho2=sqrt(real(z2)**2+imag(z2)**2) # entweder rho2=abs(z2) # oder phi2=arctan(imag(z2)/real(z2)) # entweder phi2=angle(z2) # oder rho3=abs(z3) phi3=angle(z3)
Aufgabe 2
Führe folgende Operationen aus. Geben die zusammengehörenden Rechnungen jeweils das gleiche Resultat?
- Addition zweier komplexen Zahlen:
- z1 + z2 = ?
- Multiplikation zweier komplexer Zahlen:
- z1z2 = ?
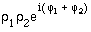 = ?
= ?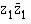 = ?
= ?- |z1| = ?
- Division zweier komplexer Zahlen:
- z1/z2 = ?
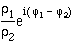 = ?
= ?- 1/z1 = ?
- z1normiert =
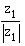 = ?
= ? - 1/z1normiert = ?
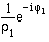 = ?
= ?
- Potenzieren einer komplexen Zahl (Moivresche Formel):
 = ?
= ?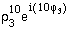 = ?
= ?
- Radizieren einer komplexen Zahl:
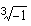 = ?
= ?
# 1.1) z1+z2 # 2.1) z1*z2 # 2.3) rho1*rho2*exp(1j*(phi1+phi2)) # 2.3) z1*conj(z1) # 2.4) abs(z1) # 3.1) z1/z2 # 3.2) (rho1/rho2)*exp(1j*(phi1-phi2)) # 3.3) 1/z1 # 3.4) z1normiert=z1/abs(z1) # 3.5) 1/z1normiert # 3.6) 1/rho1*exp(-1j*phi1) # 4.1) z3**10 # 4.2) rho3**10*exp(1j*(10*phi3)) # 5.1 -1**(1/3) # nicht was du willst (-1)**(1/3)
Aufgabe 3
Welche Funktion dreht die komplexe Zahlenebene um den Winkel 90 Grad? Verifiziere dies mit der komplexen Zahl z1.
phiz1=angle(z1, deg=True) w1=1j*z1 phiw1=angle(w1, deg=True)
Ein Physik-Beispiel
Einfache Grafiken
Du kannst Python nun verwenden um mehr oder weniger komplizierte Rechnungen auszuführen.
Als nächstes wollen wir uns aber einer typischeren Physiker-Aufgabe widmen.
Nehmen wir an, wir haben ein einfaches (simuliertes) Experiment zum freien Fall durchgeführt.
Dabei haben wir eine Kugel aus verschiedenen Höhen (1, 2, ..., 10m) fallen gelassen und
die folgenden Flugzeiten ([t]=s) gemessen:
0.43, 0.64, 0.76, 0.88, 1.00, 1.12, 1.20, 1.24, 1.33, 1.40
Wir wollen das Resultat nun graphisch Darstellen.
Als Erstes müssen wir die Zahlen in unsere Python-Session kriegen.
Wir brauchen zwei Variablen, die jeweils eine Liste mit den Werten für die Höhe
bzw. die Zeit enthält.
Eine Liste definierst du, indem du den gewünschten Listeninhalt zwischen [ ] setzt.
h = [ 1,2,3,4,5,6,7,8,9,10 ] t = [0.43,0.64,0.76,0.88,1.00,1.12,1.20,1.24,1.33,1.40 ]
Nachdem wir nun unsere beiden Variablen definiert haben, können wir die Punkte unserer Messungen zeichnen.
plot(t,h,'x')
Python stellt (durch das Modul mathplotlib) diverse Funktionen
fürs erstellen von Grafiken bereit.
Hier haben wir einfachste Funktion verwendet.
plot(x,y) zeichnet die Punkte die durch die
beiden Listen x und y definiert sind.
Der i-te Punkt wird dabei durch die i-ten Einträge der beiden Listen gegeben.
Das dritter Argument in unserem Befehl ('x'), legt fest,
dass die Punkte durch x markierte werden sollen.
Listen generieren
Die Liste oben hast du entweder kopiert oder eingetippt.
Mindestens für die Höhe, hätten wir auch eine einfachere Möglichkeit gehabt.
Listen mit regelmässigen Unterschieden werden sehr häufig gebraucht.
Mit range(start, stop, step) kannst du
Liste erzeugen.
Stop ist dabei nicht Teil der erzeugten Liste.
Das h von oben, bekommst du also mit range(1,11) (Start mit 1, Stop vor 11, Standardschrittlänge 1).
Dabei ist die Ausgabe auf den ersten Blick nicht sehr hilfreich.
So gibt Python bei range(1, 11) bloss range(1, 11) zurück.
Grund dafür ist, dass range die Werte dieser Liste erst erzeugt,
wenn du sie wirklich brauchst.
Bis dahin speichert Python einfach ein Objekt mit der Definition der Liste.
Mit list(range(10)) kannst du Python aber auch zwingen die Liste explizit auszugeben.
list(range(10)) list(range(1,10)) list(range(1,10,2)) list(range(1,10,0.1))
Wie du siehst funktioniert der letzte Befehl nicht.
Leider kann range() nur Integer-Listen erstellen.
Dank dem numpy-Modul, stehen uns aber noch weitere Befehle zur Verfügung:
arange(start, stop, step)- Array von Integer oder Float in [start, stop), Schrittlänge step.
linspace(start, stop, N)- Array von Float in [start, stop], mit N regelmässigen Punkten.
frange(start, stop, step)- Array von Float in [start, stop], Schrittlänge step.
Die Beschreibung oben spricht nicht von Listen sondern von Arrays. Der Arrays sind eine verbesserte Art von Listen die ebenfalls durch das numpy-Modul zur Verfügung gestellt werden. Wenn du die Befehle ausführst, siehst du dass unterschiedliche Objekte erzeugt werden.
list(range(10)) arange(10)
Im Output des zweiten Befehls, siehst du auch wie du selbst ein Array definieren kannst.
Du übergibst dafür dem Befehel array() eine Liste mit den gewünschten Werten.
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) array(range(10))
Wir werden uns später mehr mit den Unterschieden zwischen Arrays und Listen beschäftigen.
Aufgabe 4
Definiere folgenden Variablen:
- x1, ein Liste mit den Integer in [0,10] in 1-er Schritten.
- x2, ein Liste mit 80 Punkte gleichmässig verteilt im Interval [0,10].
- y1, ein Liste mit den Zahlen in [-10, 10] in 0.5-er Schritten.
Wie viele Einträge haben die Listen x1, x2 und y1?
(Tipp: len?)
x1=range(11) x2=linspace(0,10,80) y1=frange(-10,10,0.5) len(x1) len(x2) len(y1)
Eine Funktion darstellen
Mit dem Wissen über die range-Befehle kehren wir nun zu unserem Fall-Experiment zurück. Wir haben bisher die gemessenen Punkte gezeichnet. Um diese noch grob mit der Theorie zu vergleichen, wollen wir auch die theoretische Vorhersage einzeichnen. (Falls du das Grafikfenster bereits geschlossen hast, musst du als erstes den plot-Befehl noch einmal ausführen.) Auch für die Theorie brauchen wir zwei Listen (bzw. Arrays) mit Punkten der Kurve. Dieses mal möchten wir aber alle 0.1m einen Punkt, so dass unsere Vorhersage etwas genauer wird.
h_theorie = frange(0,10,0.1)
Als nächstes müssen wir die erwarteten Zeiten berechnen. Wir lösen also s = 0.5gt2 nach t auf, rechnen die Zeiten aus und plotten dann das Resultat.
t_theorie = sqrt(2/9.81*h_theorie) plot(t_theorie, h_theorie)
Wie du siehst, kannst du das h-Array direkt in der Rechnung verwenden. Python führt die Rechnung dann für jedes Element aus und gibt dir die Resultate wieder in einem Array zurück. Das ist einer der wichtigen Unterschiede zwischen Arrays und Listen. Mit einer Listen würde das nicht klappen.
Zum Schluss wollen wir unsere Grafik speichern und ausdrucken.
Zum Speichern klickst du auf das Disketten-Symbol.
Wähle danach das Verzeichnis, den Dateinamen und das Dateiformat.
(PDF ist für solche Grafiken wohl die beste Wahl.)
Alternativ kannst du die Grafik auch mit dem Befehl savefig('dateiname.pdf')
ins aktuelle Verzeichnis speichern.
Öffne anschliessend das PDF und drucke es aus.
Gratuliere, du hast deine erste Grafik erstellt.
Aufgabe 5
Erstelle eine analoge Grafik für folgendes Experiment:
Die Periode eines Faden-Pendels wurde für verschiedene Pendellängen gemessen.
Die Pendellänge wurde von 0.5m in 0.1m Schritten bis 1.5m erhöht.
Die folgenden Perioden wurden gemessen ([T] = s):
1.38, 1.55, 1.70, 1.77, 1.90, 2.01, 2.05, 2.22, 2.30, 2.36, 2.47
(Die Vorhersage der Theorie kannst du selbst herleiten oder zum Beispiel auf Wikipedia nachschauen.)
l_data = frange(0.5,1.5,0.1) t_data = [ 1.38, 1.55, 1.70, 1.77, 1.90, 2.01, 2.05, 2.22, 2.30, 2.36, 2.47 ] plot(l_data,t_data,'x') l_theorie = frange(0,1.5,0.01) t_theorie = 2*pi*sqrt(l_theorie/9.81) plot(l_theorie, t_theorie)
Aufgaben zur Vertiefung
Das Tutorial enthält verschiedene Aufgaben, bei denen du das Gelernte anwenden kannst. Die Aufgaben reichen aber wohl nicht aus, damit du dein Wissen wirklich festigen könntest. Die Vertiefungsaufgaben repetieren den Inhalt des Blockes deshalb ein weiteres Mal. Entscheide selbst, welche Themen du noch einmal anschauen und welche Aufgaben du lösen möchtest. Du darfst dir auch gerne selbst weitere Aufgaben stellen.
Komplexe Rechnungen
- Kontrolliere den Zusammenhang zwischen
sinundcossowie und den komplexen Zahlen für verschiedenex
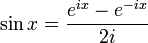 ,
, 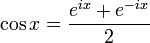
Funktionen darstellen
Erstelle Grafiken verschiedener Funktionen. Hier ein paar mögliche Beispiele:
- y = 2x2-1
- y = log(x)
- y = e-x2
- y = 32x5-32x3+6x
- y = sinh(x)
